Matematyka
(z łac. mathematicus,
od gr. μαθηματικός mathēmatikós, od μαθηματ-, μαθημα mathēmat-, mathēma,
„nauka, lekcja, poznanie”, od μανθάνειν manthánein, „uczyć się, dowiedzieć”;
prawd. spokr. z goc. mundon, „baczyć, uważać”)
– nauka dostarczająca narzędzi do otrzymywania ścisłych wniosków z przyjętych założeń, zatem dotycząca prawidłowości rozumowania. Ponieważ ścisłe założenia mogą dotyczyć najróżniejszych dziedzin myśli ludzkiej, a muszą być czynione w naukach ścisłych, technice a nawet w naukach humanistycznych, zakres matematyki jest szeroki i stale się powiększa.
Wiele dziedzin nauki i technologii, w pewnym momencie zaczyna definiować swoje pojęcia z dostatecznie dużą precyzją, aby można było stosować do nich metody matematyczne, co często zapoczątkowuje kolejny dział matematyki teoretycznej lub stosowanej. Tak stało się np. z mechaniką klasyczną, mechaniką statystyczną, ekonomią (ekonometria), lingwistyką (lingwistyka matematyczna), teorią gier, a nawet niektórymi działami politologii (teoria głosowań). Obecnie standardem w naukach eksperymentalnych jest potwierdzanie istnienia obserwowanych zależności za pomocą metod statystyki, będącej działem matematyki. Pozwala to odróżnić rzeczywiste wyniki od przypadkowej zbieżności. Leonardo da Vinci stwierdził w Traktacie o malarstwie: „Żadne ludzkie badania nie mogą być nazywane prawdziwą nauką, jeśli nie mogą być zademonstrowane matematycznie.”
Matematyka teoretyczna, nazywana czasami matematyką czystą, jest często rozwijana bez wyraźnego związku z konkretnymi zastosowaniami. W tej odmianie jest ona przez niektórych matematyków uważana za formę sztuki.fizyka lub informatyka. Szkolne rozumienie matematyki, jako nauki wyłącznie o liczbach i pojęciach geometrycznych, zdezaktualizowało się już w XIX wieku wraz z postępami algebry i teorii mnogości. Częścią nieodzowną matematyki jest logika. Jednak niektóre działy matematyki teoretycznej znalazły swoje praktyczne zastosowanie, kiedy okazało się, że potrzebuje ich nowoczesna
Definicje i wizje
- Paul Dirac stwierdził „Matematyka jest narzędziem stworzonym specjalnie do wszelkich abstrakcyjnych koncepcji i nie ma ograniczeń dla jej potęgi w tym zakresie”
- Benjamin Peirce nazwał ją „nauką, która wyciąga właściwe wnioski”
- Henri Poincaré określił matematykę jako „sztukę nadawania takich samych nazw różnym rzeczom”. Oddaje to jedną z piękniejszych cech matematyki, zdolnej uogólniać właściwości i czynić analogie między bardzo odległymi i wydawałoby się mało ze sobą związanymi obiektami.
- David Hilbert uznał, że „sztuka uprawiania matematyki zawiera się w znajdowaniu szczególnych przypadków, które zawierają w sobie zalążki uogólnień”
- Poeta William Wordsworth stwierdził: „Matematyka jest niezależnym światem stworzonym przez czystą inteligencję”
- Z czasem niektóre działy matematyki stały się odrębnymi światami, uprawianymi wyłącznie dla ich piękna, bez jakiegokolwiek związku z rzeczywistością. Henry John Stephen Smith stwierdził wprost „Czysta matematyka, oby nigdy nie była przez nikogo używana”
- Z drugiej strony Nikołaj Łobaczewski uznał, że „Nie ma gałęzi matematyki, choćby nie wiem jak abstrakcyjnej, która pewnego dnia nie zostałaby zastosowana do zjawisk realnego świata”
- Wyprzedził tą wypowiedzią o pół wieku postępy fizyki, która stosuje w praktyce działy matematyki, przed jej epoką uważane za domenę czystej myśli, niezbrukanej zastosowaniami.
- Immanuel Kant stwierdził „Matematyka jest najjaskrawszym przykładem, jak czysty rozum może skutecznie rozszerzać swoją domenę bez jakiejkolwiek pomocy doświadczenia”
Główne działy
Matematyka jest dynamiczną symbiozą dziedzin, działów czy teorii, które przenikają się oraz zależą jedne od drugich. Powstają wciąż nowe teorie, stare obumierają, a czasem znowu wracają do życia. Matematyka wymyka się klasyfikacji lub zmusza do tworzenia klasyfikacji wciąż na nowo.
Amerykańskie Towarzystwo Matematyczne prowadzi klasyfikację gałęzi matematyki, w których prowadzone są aktywne badania naukowe. Ta klasyfikacja jest uaktualniana co pewien czas, aby odzwierciedlić zmiany w zainteresowaniach matematyków, a dzisiaj obowiązująca jej wersja jest określana jako MSC 2000 (Mathematical Subject Classification 2000). MSC jest używane przez wiele czasopism matematycznych oraz baz danych w rodzaju Mathematical Reviews. Klasyfikacja ta obejmuje opisane poniżej główne gałęzie matematyki, z których każda jest dalej dzielona. Łącznie zawiera ona ponad 5000 szczegółowych dziedzin matematyki i dziedzin z matematyką związanych. Każda dziedzina ma przypisany pięcioznakowy kod.
Logika i podstawy


Podstawy matematyki definiują język matematyki, sposoby przeprowadzania dowodów matematycznych, metody budowania jej struktur i teorii oraz określają własności jej podstawowych obiektów, takich jak zbiór.
- 03Bxx Logika ogólna
- 03Cxx Teoria modeli
- 03Dxx Teoria obliczeń i teoria rekursji
- 03Exx Teoria mnogości
- 03Fxx Teoria dowodu, matematyka konstruktywna, metamatematyka
- 03Gxx Logika algebraiczna
- 03Hxx Niestandardowe modele
Algebra
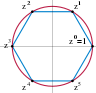


Algebra to dział matematyki zajmujący się strukturami algebraicznymi, porządkowymi, relacjami i uogólniający rozmaite własności działań wspólne dla różnych zbiorów, w których działania takie mogą być przeprowadzane.
- 05-xx Kombinatoryka i teoria grafów
- 06-xx Porządki, kraty, algebry Boole'a, uporządkowane struktury algebraiczne. Często zaliczane są one do teorii mnogości, jednak MSC inaczej je klasyfikuje.
- 08-xx Ogólne systemy algebraiczne
- 11-xx Teoria liczb
- 12-xx Teoria ciał i wielomianów
- 13-xx Pierścienie i algebry przemienne
- 14-xx Geometria algebraiczna
- 15-xx Algebra liniowa i n-liniowa; teoria macierzy
- 16-xx Pierścienie i algebry łączne
- 17-xx Niełączne pierścienie i algebry
- 18-xx Teoria kategorii często zaliczana do logiki, algebra homologiczna
- 19-xx K-teoria
- 20-xx Teoria grup i jej uogólnienia
- 22-xx Grupy topologiczne, grupy Liego
Analiza

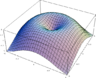

Analiza matematyczna bada pochodne, całki, miary, sumy szeregów, równania różniczkowe i inne pojęcia związane najogólniej mówiąc z przechodzeniem do granicy.
- 26-xx Teoria funkcji rzeczywistych
- 28-xx Teoria miary i całkowania
- 30-xx Funkcje zmiennej zespolonej
- 31-xx Teoria potencjału
- 32-xx Funkcje wielu zmiennych zespolonych i przestrzenie analityczne
- 33-xx Funkcje specjalne
- 34-xx Równania różniczkowe zwyczajne
- 35-xx Równania różniczkowe cząstkowe
- 37-xx Teoria układów dynamicznych i ergodyczności
- 39-xx Równania różnicowe i równania funkcyjne
- 40-xx Ciągi, szeregi
- 41-xx Aproksymacja
- 42-xx Analiza Fouriera
- 43-xx Abstrakcyjna analiza harmoniczna
- 44-xx Transformacje całkowe, rachunek operatorów
- 45-xx Równania całkowe
- 46-xx Analiza funkcjonalna
- 47-xx Teoria operatorów
- 49-xx Rachunek wariacyjny i optymalizacja
- 49-xx Analiza zespolona i Twierdzenie podstawowe Cauchy'ego
Geometria



Geometria zajmowała się kolejno przestrzeniami euklidesowymi, sferycznymi, afinicznymi i rzutowymi, hiperbolicznymi, ogólniej rozmaitościami Riemanna i w końcu stałą się dziedziną badającą dla wybranych przekształceń ich niezmienniki, od najprostszych, takich jak odległość, pole powierzchni, miara kąta, przez bardziej zaawansowane, jak krzywizna, punkt stały, czy wymiar.
- 51-xx Geometria
- 52-xx Geometryczne pojęcie wypukłości, wielotopy, geometria dyskretna
- 53-xx Geometria różniczkowa
Topologia



Topologia (zwana początkowo geometria situs, „geometrią położenia” lub analysis situs, „analizą położenia”) w elementarnej wersji jest nauką badającą te właściwości geometryczne, które nie zmieniają się przy przekształceniach takich jak rozciąganie, skręcanie albo obroty. Do własności takich należy na przykład liczba otworów, jakie znajdują się w danej bryle geometrycznej.
- 54-xx Topologia ogólna
- 55-xx Topologia algebraiczna, teoria homologii, teoria homotopii
- 57-xx Rozmaitości topologiczne i kompleksy komórkowe, teoria węzłów
- 58-xx Analiza globalna, analiza na rozmaitościach
Matematyka dyskretna



Często (choć nie w MSC) wyróżnia się oddzielnie grupę dziedzin, które badają struktury nieciągłe, sprowadzające się do zbiorów przeliczalnych. Do matematyki dyskretnej zalicza się m.in. (wymienione także w odpowiednich miejscach klasyfikacji MSC)
- kombinatoryka
- kryptologia
- logika matematyczna
- programowanie liniowe
- teoria gier (pewne działy)
- teoria grafów
- teoria informacji (elementarna jej część)
- teoria liczb (po części)
- teoria matroidów
- teoria węzłów (częściowo)
- teoria konfiguracji
- geometria skończona
- algorytmika
- teoria złożoności
Statystyka i rachunek prawdopodobieństwa


Statystyka zajmuje się wnioskowaniem o całej populacji nieco różniących się obiektów (np. ludzi) na podstawie obserwacji części tej populacji (tzw. próby statystycznej).
- 60-xx Rachunek prawdopodobieństwa i procesy stochastyczne
- 62-07 Analiza danych
- 62-09 Metody graficzne statystyki
- 62Cxx Teoria decyzji
- 62D05 Teoria próbkowania
- 62Exx Rozkłady prawdopodobieństwa
- 62Fxx Teoria estymacji
- 62Gxx Statystyka nieparametryczna
- 62Hxx Analiza danych wielowymiarowych
- 62Jxx Metody liniowe statystyki
- 62Kxx Projektowanie eksperymentów
- 62Lxx Metody sekwencyjne statystyki
- 62Mxx Wnioskowanie z procesów stochastycznych
- 62Nxx Analiza przeżycia
- 62Pxx Zastosowania statystyki
Matematyka stosowana


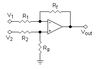
Matematyka stosowana jest nauką rozwijającą aparat matematyczny na potrzeby innych nauk i techniki.
- 65-xx Analiza numeryczna
- 68-xx Informatyka matematyczna, teoria obliczeń, algorytmy, teoria złożoności
- 70-xx Mechanika cząstek i układów
- 74-xx Mechanika ciał deformowalnych
- 76-xx Zastosowania matematyki w mechanice płynów
- 78-xx Zastosowania matematyki w optyce i elektromagnetyzmie
- 80-xx Zastosowania matematyki w termodynamice klasycznej
- 81-xx Mechanika kwantowa
- 82-xx Mechanika statystyczna, budowa materii
- 83-xx Teoria względności
- 85-xx Zastosowania matematyki w astronomii i astrofizyce
- 86-xx Zastosowania matematyki w geofizyce
- 90-xx Badania operacyjne, programowanie matematyczne
- 91-xx Teoria gier, ekonomia, nauki społeczne
- 92-xx Biomatematyka i matematyka w innych naukach przyrodniczych
- 93-xx Teoria systemów, teoria sterowania
- 94-xx Teoria informacji, teoria sygnałów, korekcja błędów, teoria obwodów, zbiory rozmyte
- 97-xx Edukacja matematyczna
- 98-xx Geometria wykreślna
- 99-xx Rachunek wyrównawczy
Badania okołomatematyczne
MSC wyróżnia także dziedziny, które zajmują się samą matematyką jako przedmiotem swojego zainteresowania.
- 00-xx Badania ogólne, filozofia matematyki, rozrywka matematyczna
- 01-xx Historia matematyki, biografie matematyków
Struktura formalna
Matematyka jest sztuką wyciągania wniosków z założeń. Jeśli rozumowanie matematyczne jest poprawne, to przy poprawnych założeniach istnieje pewność otrzymania poprawnych wniosków. Jeśli w rozumowaniu jest jakakolwiek nieścisłość, takiej gwarancji nie ma. Stąd wynika olbrzymi nacisk, kładziony w matematyce na ścisłość rozumowania. W utrzymaniu tej ścisłości pomaga omawiany dalej formalizm logiczny oraz zapis matematyczny.
Nie znaczy to, że w matematyce wyobraźnia, głębia, czy intuicja nie są ważne. Matematyka nie może sensownie istnieć bez aparatu formalnego, ale formalizm tworzy tylko ramy dla inwencji i twórczego myślenia matematyka, podobnie jak gramatyka języka tworzy ramy dla inwencji pisarza. Formalizm, choćby w praktyce tylko przybliżony, jest metodą obiektywnego porozumiewania się matematyków. Można używać do omawiania pojęć matematycznych zwykłego języka naturalnego, jednak ma to sens tylko tak długo, jak długo da się taki opis jednoznacznie przetłumaczyć na formalizm (nawet jeśli to tłumaczenie nie jest w praktyce wykonane).
Formalna struktura matematyki wygląda następująco:
- Wybierany jest tzw. alfabet złożony ze skończonej liczby rozróżnialnych znaków (np. liter, cyfr, znaków matematycznych, itp.).
- Tworzony jest język formalny, na który składają się słowa złożone ze znaków alfabetu.
- Słowa tworzą wyrażenia, w tym zdania. Praktyczne teorie powinny pozwalać na mechaniczne (algorytmiczne) sprawdzanie, które ciągi symboli tworzą poprawnie zbudowane zdania oraz mieć jednoznaczną, dającą się algorytmicznie rozpoznać składnię.
- Formalne języki służą za podstawę teoriom formalnym (wciąż ogólniejszym od matematycznych). Teoria formalna oprócz języka wprowadza pojęcie twierdzenia (specjalny rodzaj zdań poprawnie zbudowanych) i reguł dowodzenia.
- Jedną z teorii formalnych jest logika matematyczna. Te z formalnych teorii, które zawierają logikę matematyczną, nazywane są teoriami matematycznymi. Większość teorii matematycznych zawiera też teorię mnogości. Wraz z logiką matematyczną (klasyczną) przychodzi formalne pojęcie prawdy, które można zdefiniować na wiele sposobów.
- Teorią matematyczną nazywany jest formalnie dowolny niesprzeczny zbiór zdań. W praktyce z symboli języka formalnego wydziela się tzw. pojęcia pierwotne. Na tym etapie o pojęciach pierwotnych nic jeszcze nie wiadomo. Na przykład pojęciami pierwotnymi dwuwymiarowej geometrii euklidesowej są punkt, prosta i relacja incydencji („punkt leży na prostej”, bądź „prosta zawiera punkt” – bez wyróżniania prostej, czy punktu).
- Zwykle budowana jest tzw. aksjomatyka, czyli wyróżniany jest zestaw zdań zwanych aksjomatami, mówiących o relacjach między pojęciami pierwotnymi. Dla geometrii euklidesowej jednym z aksjomatów jest zdanie: „Przez każde dwa punkty można przeprowadzić prostą”.
- Używając reguł wnioskowania, można rozpoczynając od aksjomatów dowodzić rozmaitych twierdzeń danej teorii.
- Teoria nie musi (i nie może) w żaden sposób odnosić się do innych cech pojęć pierwotnych niż te, które zostały wyrażone przez aksjomaty lub z nich wynikają. Jeśli jakieś pojęcia zostaną zdefiniowane w taki sposób, aby podstawione w miejsce pojęć pierwotnych teorii spełniały jej aksjomaty – operacja ta nazywa się interpretacją – twierdzenia teorii będą prawdziwe także dla tych nowo zdefiniowanych pojęć. Taki zestaw interpretacji pojęć pierwotnych nazywany jest modelem danej teorii. Modelem płaskiej geometrii euklidesowej jest np. kartezjański układ współrzędnych (ściślej tzw. przestrzeń kartezjańska), gdzie punkt interpretowany jest jako para liczb rzeczywistych (zwanych współrzędnymi), prosta – jako zbiór punktów P = (x,y) spełniających dla pewnych punktów A = (xA,yA) oraz B = (xB,yB) równanie (yA − yB)(x − xB) − (xA − xB)(y − yB) = 0, natomiast relację incydencji interpretuje się jako relację przynależności do tego zbioru.
- Powyżej teoria matematyczna była opisywana z bardzo formalnego punktu widzenia, tzn. przez pryzmat operacji na symbolach matematycznych. Matematycy jednak zwykle nie wyobrażają sobie matematyki w ten sposób. Rozumują raczej w kategoriach przestrzeni i struktur, składających się z pewnego zbioru elementów (np. liczb) oraz działań i relacji między nimi (np. relacje porządku i działania algebraiczne). Zbiory wraz z różnego rodzaju powiązaniami pomiędzy ich elementami zwane są właśnie strukturami lub przestrzeniami. Na poziomie formalnym pojęcia te są synonimami pojęcia modelu, jednak koncepcyjnie podejście to ułatwia skoncentrowanie się na bardziej uchwytnych obiektach (elementach przestrzeni), niż na formalnych manipulacjach symbolami.
W praktyce matematycy nie przejmują się zanadto powyższym formalizmem podczas rozszerzania danej teorii (a więc, formalnie, tworzenia nowej). Poprawne (w sensie praktycznym) dowody matematyczne są jednak w odczuciu matematyków sprowadzalne do dowodów formalnych. Obecnie rozwija się formalizację matematyki opartą na metodach informatycznych, która pozwala na pełny formalny zapis dowodów dający się stosować w praktyce.
Zapraszamy do zapisania się na nasz newsletter !
